Category: teaching

Quantum States in Argand Diagrams: vacuum, coherent, and squeezed

If you need to admire complex analysis for its elegance and visual utility, try quantum optics. Specifically, the description of quantum states. Thanks to creation and annihilation operators, the position and momentum states of a quantum optical field can be represented as quadratures. These entities can now be represented on the orthogonal axes of a complex plane. The representation of Argand diagrams starting with a classical electromagnetic field and then extrapolating them to quantum theory is a tribute to its geometrical representation. The fact that two axes can be utilized to represent real and imaginary parts of the defined state is itself an interesting thing. By certain operations within the plane, one can realize the vacuum state, the coherent state, and the squeezed state of quantum optics.

The Vacuum Spread – One of the major consequences of quantum theory, and especially the second quantization, is the realization of the vacuum states. Even when there are zero photons, there is a residual energy in the system that manifests as vacuum states. How to define the presence or absence of a photon is a different proposition because vacuum states are also associated with something called virtual photons. That needs a separate discussion. Anyway, in a complex plane of quadrature, a vacuum state is represented by a circular blob and not a point (see fig. 1). It is the spread of the blob that indicates the uncertainty. In a way, it is an elegant representation of the uncertainty principle itself because the spread in the plane indicates the error in its measurement. Importantly, it emphasizes the point that no matter how low the energy of the system is, there is an inherent uncertainty in the quadrature of the field. This also forms the fundamental difference between a classical and a quantum state. The measurement of the vacuum fluctuation is a challenging task, but one of the most prevalent consequences of vacuum fluctuation is the oblivious spontaneous emission. If one looks at the emission process in terms of stimulated and spontaneous pathways, then the logical consequence of the vacuum state becomes evident in some literature on quantum optics. Spontaneous emission is also defined as stimulated emission triggered by vacuum state fluctuations. It is an interesting viewpoint and helps us to create a picture of the emission process vis-à-vis the stimulated emission.

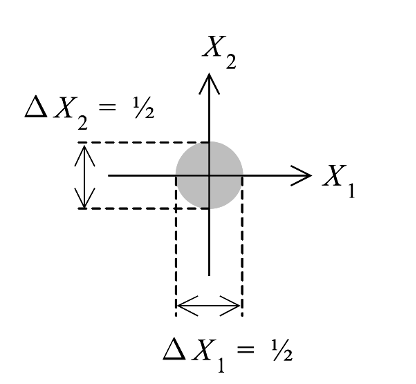
Figure 1. Vacuum state representation. Note that their centre is at the origin and has a finite spread across all the quadrants. Figure adapted from ref. 2.

Another manifestation of the vacuum state is the Casimir effect, where an attractive force is induced as you bring two parallel plates close to each other. The distance being of the order of the wavelength or below this triggers a fascinating phenomenon which has deep implications not only in understanding the fundamentals of quantum optics and electrodynamics, but also in the design and development of quantum nanomechanical devices.

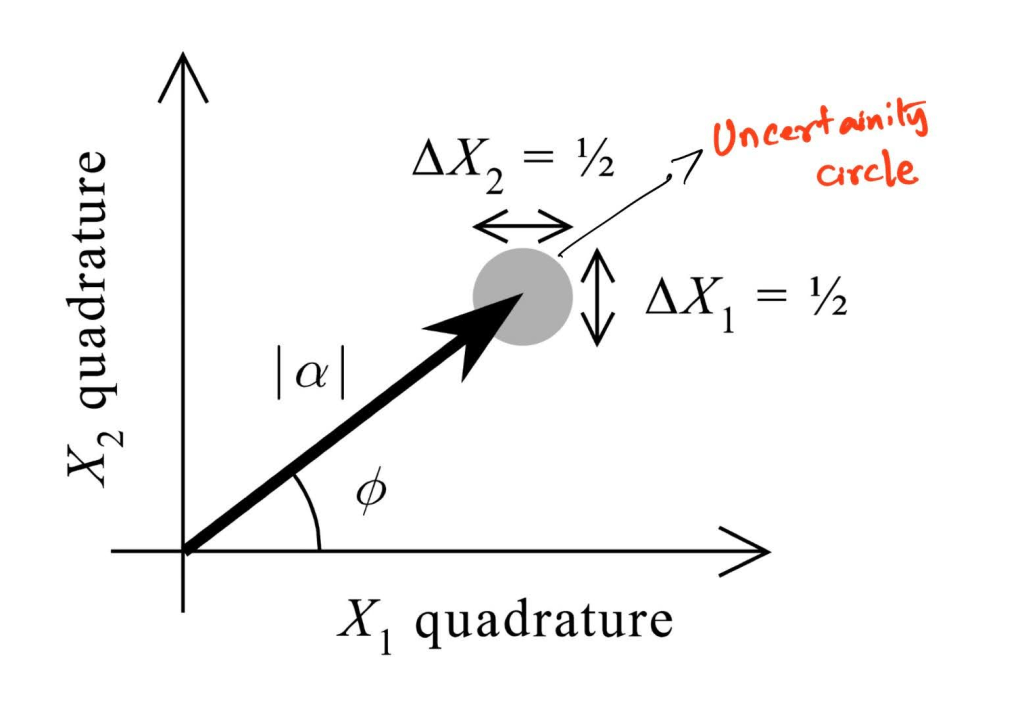
A shift in the plane – Coherent states are also described as displaced vacuum states, and this displacement is evident in the Argand diagrams. The quadrature can now help us visualize the uncertainty in the phase and the number of photons in the optical field. One of the logical consequences of the coherent state is the number-phase uncertainty. This gets clear if one observes the spread in the angle of the vector and the radius of the blob represented (see Fig. 2). Notice that the blob still exists. The only difference is that the location of the blob has shifted. The consequence of this spread has a deeper connection to the uncertainty in the average number of photons and the phase of the optical field. The connection to the number of photons is through the mod alpha, which essentially represents the square root of the average number of photons. Taken together, the blob in the Argand diagram represents the number-phase uncertainty.

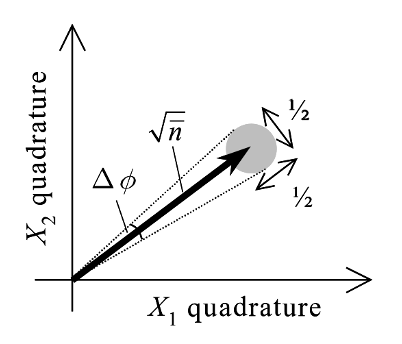
Figure 2.  Coherent state representation. Note that their centre is displaced. Figure adapted from ref. 2.

Lasers are the prototypical examples of coherent states. The fact that they obey Poissonian statistics is the direct consequence of the variance in the photon number, which is equivalent to the square root of the average number of photons. This means one can use photon statistics to discriminate between sources that are sub-Poissonian, Poissonian, or super-Poissonian in nature. The super-Poissonian case is the thermal light, and the sub-Poissonian state represents photon states whose number can reach up to 1 or 0. The coherent states sit in the middle, obeying the Poissonian statistics.

Everything has a cost – Once you have a circle with a defined area, it will be interesting to ask: Can you ‘squeeze’ this circle without changing its area? The answer is yes, and that is what manifests as a squeezed state. In this special state, one can squeeze the blob along one of the axes at the cost of a spread in the orthogonal direction. This converts the circle into an ellipse (see Fig. 3).

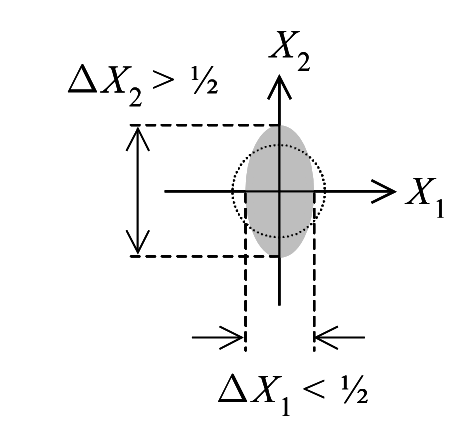
Figure 3. Squeezed State. Note the circle has been squeezed into an ellipse. Figure adapted from ref. 2.

Note that the area must be conserved, which means that the uncertainty principle still holds good; just that the reduction in the uncertainty along one axis is compensated by the increment in another. This geometrical trick has a deep connection to the behaviour of an optical field. If one squeezes the axis along the average number of photons, it means that you are able to create an amplitude-squeezed state. This means the uncertainty in the counting of photons in that state has reduced, albeit at the cost of the uncertainty in the measurement of phase. Similarly, if one squeezes the blob along the axis of the phase, then we end up with a lowering of the uncertainty for the optical phase. Of course, this comes at the cost of counting of number of photons. I should mention that the concept of optical phase itself is not clearly defined in quantum optics. This is because an ill-defined phase can have a value of 2π, which creates the problem. An interesting application of the phase-squeezed quantum states is in interferometric measurements. By reducing the uncertainty in the phase, one can create highly accurate measurements of phase shifts. So much so that this can have direct implications on high-precision measurements, including gravitational wave detection. The anticipation is also that such tiny shifts can be helpful in observing feeble fluctuations in macroscopic quantum systems.

Pictures can lead to more than 1,000 words. And if you add them to a quantum optical description, as in the case of the states that I have defined, they create a quantum tapestry. Perhaps this is the beauty of physics, where there is a coherence between mathematical language, geometrical representation, and physical reality. Feynman semi-jokingly may have said, “Nobody understands quantum mechanics,” but he forgot to add that there is great joy in the process of understanding through mathematical pictures. After all, he knew the power of diagrams.

References:

  1. Ficek, Zbigniew, and Mohamed Ridza Wahiddin. Quantum Optics for Beginners. 1st edition. Jenny Stanford Publishing, 2014.
  2. Fox, Mark. Quantum Optics: An Introduction. Oxford Master Series in Physics 15. Oxford University Press, 2006.
  3. Gerry, Christopher C., and Peter L. Knight. Introductory Quantum Optics. Cambridge, United Kingdom ; New York, NY, 2024.
  4. Saleh, B. E. A., and M. C. Teich. Fundamentals of Photonics. 2nd edition. Wiley India Pvt Ltd, 2012.

Brillouin on Sommerfeld

“Everybody wondered (and still wonders) why the Stockholm committee systematically ignored Sommerfeld’s pioneer work in modern physics. Such an omission is actually impossible to understand.”

Leon Brillouin, in the foreword of his book WAVE PROPAGATION AND GROUP VELOCITY (1959)

Brillouin further mentions the teachers who taught him, and rates Sommerfeld among the best:

“I had the great privilege of attending, as a student, lectures given by some prominent physicists, such as H. A. Lorentz, H. Poincaré, and P. Langevin. But I was especially impressed by Sommerfeld’s mastery as a teacher.“

Teaching & Meaning

What adds meaning to my academic work?

Perhaps, an anonymous feedback on your teaching is one of them….

“very well taught course at a well defined pace. The interesting way various different aspects and fields in Optics was introduced was fascinating, made us so very keen on knowing more! The mind maps at the beginning of every topic, the indexes professor made was a great way to keep the bigger picture in mind and helped us glide through it. The assignment was also a great way to make us go through materials without feeling it it be imposing, rather finding it more interesting! Thank you so much Sir for this amazing course, the enthusiastic way in which you taught, all the great conversations you engaged in with us, and opened our eyes to explore so much more in this field! thank you!!“

I had a diverse class (BS-Physics majors, MS Quantum Tech, iPhD) with 110+ students, and I am glad a lot of students enjoyed the course this time.
I am a bit overwhelmed by the positive feedback I received on my teaching methods. For sure, I learnt about the subject as much as they did.

And as I always say: there is more to learn…for all of us..

Human interaction zindabad :-)

Quantum Optics – teaching in Jan 2026

More than 22 years ago, I started my journey as a research student in theoretical physics – Quantum Electrodynamics (QED) + Radiative Transfer (MSc summer project at the Indian Institute of Astrophysics), and my special paper in the MSc final semester was QED. Later in my PhD, I branched into experiments on light scattering (Raman, Mie & Rayleigh).

Over the years, QED and quantum optics have always been at the back of my mind while studying, researching and teaching.

Come January, I will be teaching a course on Quantum Optics to MS(Quantum Tech), MS-PhDs, and 4th-year physics UGs

I designed the first course on this topic at IISER Pune about a decade ago with the able inputs from Prof. Rajaram Nityananda, and I have taught the course a few times. Now, after a few years, I will teach it again.

With the emergence of quantum sci & tech, there is a new impetus and excitement on this topic.

Having said that, the foundations of the topic remain the same, and Quantum Optics has a wonderful history and philosophy associated with it…and where better to start than Dirac’s classic (see below).

Look out for ‘quantum blogs’ in 2026…

Humanizing Science – A Conversation with a Student

Recently, I was talking to a college student who had read some of my blogs. He was interested in knowing what it means to humanize science. I told him that there are at least three aspects to it.

First is to bring out the wonder and curiosity in a human being in the pursuit of science. The second was to emphasize human qualities such as compassion, effort, mistakes, wrong directions, greed, competition and humour in the pursuit of science. The third thing was to bring out the utilitarian perspective.

The student was able to understand the first two points but wondered why utility was important in the pursuit of humanizing science. I mentioned that the origins of curiosity and various human tendencies can also be intertwined with the ability to use ideas. Some of the great discoveries and inventions, including those in the so-called “pure science” categories, have happened in the process of addressing a question that had its origin in some form of an application.

Some of the remarkable ideas in science have emerged in the process of applying another idea. Two great examples came into my mind: the invention of LASERs, and pasteurization.

I mentioned that economics has had a major role in influencing human ideas – directly or indirectly. As we conversed, I told the student that there is sometimes a tendency among young people who are motivated to do science to look down upon ideas that may have application and utility. I said that this needs a change in the mindset, and one way to do so is to study the history, philosophy and economics of science. I said that there are umpteen examples in history where applications have led to great ideas, both experimental and theoretical in nature, including mathematics.

Further, the student asked me for a few references, and I suggested a few sources. Specifically, I quoted to him what Einstein had said:

 “….So many people today—and even professional scientists—seem to me like someone who has seen thousands of trees but has never seen a forest. A knowledge of the historic and philosophical background gives that kind of independence from prejudices of his generation from which most scientists are suffering. This independence created by philosophical insight is—in my opinion—the mark of distinction between a mere artisan or specialist and a real seeker after truth..”

The student was pleasantly surprised and asked me how this is connected to economics. I mentioned that physicists like Marie Curie, Einstein and Feynman did think of applications and referred to the famous lecture by Feynman titled “There is Plenty of Room at the Bottom” (1959).

To give a gist of his thinking, I showed what Feynman had to say on miniaturization:

“There may even be an economic point to this business of making things very small. Let me remind you of some of the problems of computing machines. In computers we have to store an enormous amount of information. The kind of writing that I was mentioning before, in which I had everything down as a distribution of metal, is permanent. Much more interesting to a computer is a way of writing, erasing, and writing something else. (This is usually because we don’t want to waste the material on which we have just written. Yet if we could write it in a very small space, it wouldn’t make any difference; it could just be thrown away after it was read. It doesn’t cost very much for the material).”

I mentioned that this line of thinking on minaturization is now a major area of physics and has reached the quantum limit. The student was excited and left after noting the references.

On reflecting on the conversation, now I think that there is plenty of room to humanize science.

Random Walks in Polarization

I have been teaching polarization of light in my optics class. In there, I introduced them to matrix representation of polarization states. One of the standard references that I use for explanation is a 1954 paper in American J. Physics, by McMaster titled: “Polarization and the Stokes Parameters.”

While skimming through the pdf of the journal paper, I found an excerpt from a 1954 book, which quotes Fresnel writing to Thomas Young:

Further, I knew from the past that S. Chandrasekhar (astrophysicist) had a role in rejuvenating Stokes vector formalism in radiative transfer. Below is his description from AIP oral history archives (May 1977):

” I started the sequence of papers, and almost at the time I started it, I read the paper by Wick in which he had used the method of discrete coordinates,* and I realized at once that that method can be used in a large scale way for solving all problems. So that went on. I have always said and felt that the five years in which I worked on radiative transfer [1944 – 49] is the happiest period of my scientific life. I started on it with no idea that one paper would lead to another, which would lead to another, which would lead to another and soon for some 24 papers — and the whole subject moved with its own momentum.” (emphasis added)

He further states how he rediscovered Stokes polarization vector formalism:

“All this had a momentum of it own. Then suddenly I realized one had to put polarization in; the problems of characterizing polarized light — my rediscovery of Stokes original paper, writing on Stokes parameters and calling them Stokes parameters for the first time“

Chandra further adds that the Stokes formalism was almost forgotten for 50 years, and he had a role in resurrecting it.

Next, there was some noise on social media where some one questioned the utility of matrix multiplication. For them, below is a wonderful review article by McMaster (again), to explore from polarization viewpoint, and realize the power of non-commutative matrix algebra:

Finally, the original paper by Stokes on his formalism, which is hard to find (thanks to paywall). But, classic papers are hard to suppress, and I found the full paper on internet archives.

Below is a snapshot:

Enjoy your random walk !

Gardner’s Synthesis

Once in a while, during my research, I come across writing by scholars from other disciplines that gives me a perspective that not only helps me to grasp the complexity of learning across disciplines, but also resonates with some thoughts on education.

Howard Gardner is one such academic who works on developmental psychology and has researched extensively on cognition and education. He has written ~30 books and ~1000 articles, and blogs regularly, even at the age of 82 or so. His recent book is titled A Synthesizing Mind.

Howard Gardner is a renowned Harvard academic and, as his book describes him as follows:

“Throughout his career, Gardner has focused on human minds in general, or on the minds of particular creators and leaders. Reflecting now on his own mind, he concludes that his is a ‘synthesizing mind’—with the ability to survey experiences and data across a wide range of disciplines and perspectives. The thinkers he most admires—including historian Richard Hofstadter, biologist Charles Darwin, and literary critic Edmund Wilson—are exemplary synthesizers. Gardner contends that the synthesizing mind is particularly valuable at this time and proposes ways to cultivate a possibly unique human capacity.”

While exploring the book and the related material, I came across an interview with Howard Gardner. In there, he is conversing about the theme of the book and discusses the synthesis of thought across disciplines. One of the pertinent aspects of learning is to know how innovation can be fostered by cross-disciplinary exploration without diluting disciplinary rigour. As Gardner says:

“I am not opposed to disciplinary learning—indeed I am an enthusiastic advocate. Any person would be a fool to try to create physics or psychology or political science from the start. But if we want to have scholars or professionals who are innovative, creative—and innovation is not something that we can afford to marginalize—then they cannot and should not be slaves of any single discipline or methodology.”

As a physicist, I can relate to this thinking within my discipline, and how innovative ideas, over the ages, have emerged by bringing ideas from mathematics, engineering and biology into physics. Particularly, the combination of biology, physics and mathematics is one of the most exciting frontiers of human exploration today, and Gardner’s words apply well in this scenario.

Going beyond science, I am always intrigued and amazed by artists (especially musicians) who can create art that simultaneously draws the attention of specialists and generalists. This is not a trivial achievement, and as a scientist, I am always trying to understand how artists resonate so well with the public. Gardner, in the abovementioned interview, frames this problem by looking at the goals of science and arts, and draws a contrast that is worth noting:

“Most scholars and observers like to emphasize the similarities between the arts and the sciences, and that is fine. But the goals of the two enterprises are different. Science seeks an accurate and well supported description of the world. The arts seek to capture and convey various aspects of experience; and they have no obligation other than to capture the interest and attention of those who participate in them.

Of course, there are some individuals who excel in both science and art (Leonardo is everyone’s favorite example). But most artists—great or not—would not know their way around a scientific laboratory. And most scientists—even if they like to play the violin or to draw caricatures or to dance the tango—would not make works of art or performances that would interest others.”

I partially agree with this assessment, as I know a few scientists who are deeply involved in various forms of art (including music) and do it very well, even at the professional level. In a way, Gardner is re-emphasizing the “two cultures” debate of C.P. Snow. My own thoughts on this viewpoint are ambivalent, as I see science, arts and sports as important pursuits that cater to different facets of the human mind. Of course, when it comes to expertise, the division may matter. There is a lot more to learn about the interface of art and science, at least for me.

Anyway, Gardner is a fabulous writer, and his blogs and books are worth reading (and studying) if one is seriously interested in understanding how to synthesize thought across disciplines.

Since we are discussing synthesis of thought, which is a kind of harmony, and coming together, let me end the blog with a line from Mankuthimmana Kagga by the Kannada poet-philosopher D.V. Gundappa:

“ಎಲ್ಲರೊಳಗೊಂದಾಗು ಮಂಕುತಿಮ್ಮ” (Eladaralongodhagu manku thimma)

which loosely translates to: oh fool…be one among all (blend into world, living in harmony).

Harmony of disciplines and minds – how badly the world needs it today?

Real is imaginary and vice versa

This week in my optics class, I have been teaching Kramers-Kronig (KK) relations of electric susceptibility. It is fascinating to see the causality argument emerge from the relationship between the real and imaginary parts of the complex susceptibility. Whereas the time domain explanation is relatively easier to appreciate (that dissipation follows perturbation in time), for me, the frequency domain implication in KK relation is fascinating: the fact that information about the real part of the function at all frequencies can give you insight into the imaginary part at any given frequency (and vice versa) makes it such a powerful mathematical and physical tool. For example, by knowing the absorption spectrum of a medium, you can find out the refractive index of a medium at a particular frequency that is not easily accessible in experiments.

Two inferences I draw:

1) Complex analysis combined with differential calculus is one of the most beautiful and powerful mathematical tools invented, and exploring its application in experimental scenarios has made physics intriguing, useful, and profound.

2) The KK relationship shows how causality and the structure of matter are connected to each other, and by studying them, one will be able to extrapolate the idea beyond the problem at hand and apply it to a different context in physics. It just shows how ideas hop from one domain to another and how mathematics plays a critical role in intellectual arbitrage.

Real is imaginary and vice versa. Complex numbers zindabad!

Light as EM wave – in Maxwell’s words

Every year, I teach an optics course to physics majors (including physics iPhD students and MS Quantum Tech students). In the process of introduction, I discuss how light was discovered to be an electromagnetic wave. One of the thrills of this topic is to quote Maxwell from his legendary 1865 paper1, in which he makes this monumental connection. Every time I teach this, I get an intellectual kick, even after doing this for almost 1.5 decades.

The highlighted text is the famous statement. Before that, Maxwell compares his result with two experimental results and confirms his prediction. I follow this up with Hertz’s experiment.

Note: Electric waves and telegraphy were already known before Maxwell’s paper. There were papers that discussed about velocity of light and its connection to electric waves. See this paper2, for example. However, these interpretations were not as comprehensive as Maxwell’s case, and importantly, the field theory viewpoint needed Faraday’s experiments and Maxwell’s interpretation.

  1. Maxwell, James Clerk. 1865. “VIII. A Dynamical Theory of the Electromagnetic Field.” Philosophical Transactions of the Royal Society of London 155 (January): 459–512. https://doi.org/10.1098/rstl.1865.0008.
    ↩︎
  2. https://www.ifi.unicamp.br/~assis/Weber-Kohlrausch(2003).pdf ↩︎